Модель солнце – Стандартная солнечная модель

Содержание

Стандартная солнечная модель Википедия

Стандартная солнечная модель (англ. Standard solar model) — математическое представление Солнца в виде газового шара (в различной степени ионизации), в котором водород во внутренней области становится полностью ионизованной плазмой. Данная модель, являющаяся сферически-симметричной квазистатической моделью звезды, обладает структурой, описываемой несколькими дифференциальными уравнениями, выводимыми из основных принципов физики. Данная модель имеет ограничения в виде граничных условий, а именно светимости, радиуса, возраста и состава Солнца, которые определены достаточно точно. Возраст Солнца нельзя измерить напрямую; одним из способов его оценки является возраст старейших метеоритов и модели эволюции Солнечной системы.^[1] Состав фотосферы современного Солнца включает по массе 74,9% водорода и 23,8% гелия.^[2] Все более тяжёлые элементы, называемые в астрономии металлами, заключают менее 2 процентов массы. Стандартная солнечная модель используется для тестирования теории звёздной эволюции. В действительности единственным способом определения двух свободных параметров модели звёздной эволюции (содержание гелия и масштаб перемешивания) является вписывание модели в наблюдательные данные.

Калибровка солнечной модели

Считается, что звезда обладает нулевым возрастом, когда по предположениям она обладает однородным составом и только начинает создавать большую часть излучения при ядерных реакциях; таким образом, мы пренебрегаем временем сжатия из газопылевого облака. Для создания стандартной модели рассматривается звезда массой одна масса Солнца при нулевом возрасте и численно оценивается её эволюция до текущего возраста Солнца. Содержание химических элементов при нулевом возрасте оценивается по составу наиболее древних метеоритов.^[2] Наряду с информацией о содержании элементов, разумная оценка светимости при нулевом возрасте (такая как текущая светимость Солнца) переводится итеративно в корректное значение для модели; температура, давление и плотность вычисляются при решении уравнений звёздной структуры в предположении стационарного состояния звезды. Затем производятся численные расчёты параметров до момента текущего возраста звезды. Отличие измеренных значений светимости, содержания тяжёлых элементов на поверхности и других параметров от предсказанных в рамках модели может использоваться для уточнения модели. Например с момента образования Солнца некоторое количество гелия и более тяжёлых элементов исчезло из фотосферы вследствие. В результате фотосфера Солнца в настоящее время содержит приблизительно 87% от количества гелия и тяжёлых элементов в протозвёздной солнечной атмосфере. На стадии протозвезды фотосфера содержала 71.1% водорода, 27.4% гелия и 1.5% металлов.

[2] Для создания более точной модели требуется лучше знать параметры диффузии.

Численное моделирование уравнений звёздной структуры

Дифференциальные уравнения строения звёзд, такие как уравнение гидростатического равновесия, численно интегрируют. Дифференциальные уравнения в данном случае приближаются разностными уравнениями. Звезду представляют совокупностью сферических оболочек, численное интегрирование проводится по величине малых приращений радиусов оболочек с применением уравнения состояния, что даёт соотношения на давление, прозрачность и темп производства энергии в зависимости от плотности, температуры и химического состава.

[3]

Эволюция Солнца

Ядерные реакции в ядре Солнца меняют его химический состав при переработке в ядре водорода в гелий в ходе протон-протонных реакций и (в меньшей степени в Солнце и в большей степени в массивных звёздах) в CNO-цикле. При этом молекулярный вес вещества в ядре возрастает, что приводит к снижению давления. Поскольку ядро начинает сжиматься, то снижение давления в целом не происходит. По теореме вириала половина гравитационной потенциальной энергии, выделившейся при сжатии, уходит на разогрев ядра, а другая половина излучается. По закону для идеального газа данное повышение температуры также приводит к повышению давления, благодаря чему восстанавливается гидростатическое равновесие. Светимость Солнца повышается при увеличении температуры, что приводит к увеличению темпа ядерных реакций. Внешние слои расширяются для компенсирования повышения градиентов температуры и давления, поэтому радиус также увеличивается.

[3]

Ни одна из звёзд в целом не является статичной, но звёзды остаются на главной последовательности в течение долгого времени. Солнце провело на главной последовательности приблизительно 4,6 млрд лет и станет красным гигантом через 6,5 млрд лет,^[4] при этом полное время жизни составляет 11 млрд (10¹⁰) лет. Следовательно, приближение стационарного состояния является хорошим приближением. Для упрощения уравнения звёздной структуры записывают без явной зависимости от времени, за исключением уравнения для градиента светимости:

dLdr=4πr2ρ(ϵ−ϵν).{\displaystyle {\frac {dL}{dr}}=4\pi r^{2}\rho \left(\epsilon -\epsilon _{\nu }\right).}

Здесь L — светимость, ε — темп создания энергии на единицу массы, ε_ν — светимость вследствие испускания нейтрино. Медленная эволюция Солнца на главной последовательности определяется по изменению соотношения количества атомов разного вида (в основном уменьшается содержание водорода и увеличивается количество кислорода). Скорости протекания различных ядерных реакций оцениваются в рамках экспериментов в физике частиц высоких энергий и экстраполируются обратно к низким энергиям внутренних областей звёзд (Солнце сжигает кислород относительно медленно). С исторической точки зрения ошибки в скорости ядерных реакций являлись источниками крупнейших ошибок моделирования звёзд. Для определения содержания химических элементов применяются компьютерные вычисления. Некоторые виды ядер будут обладать собственными темпами создания и разрушения, поэтому требуется определять их количество на протяжении всего времени эволюции при различных условиях на температуру и плотность.

Согласно теореме Фогта-Расселла, распределение массы и химического состава внутри звезды однозначно определяет радиус, светимость и внутреннюю структуру звезды, а также последующую эволюцию (хотя теорема изначально должна была описывать только медленные устойчивые этапы звёздной эволюции и не соответствовала переходам от одного этапа эволюции к другому).^[3]

Информация о меняющемся со временем содержании различных частиц и уравнения состояния являются достаточными сведениями для численного решения уравнений структуры звезды при использовании малых приращений времени и итерирования.

Цели стандартной солнечной модели

Цели создания стандартной солнечной модели следующие:

предоставление оценки содержания гелия и величины масштаба перемешивания при согласовании параметров модели с оценками светимости и радиуса звезды в том же возрасте, что и Солнце.
предоставление способа оценки более сложных моделей с дополнительными эффектами, такими как вращение, магнитные поля и диффузия или уточнение явления конвекции, моделирование турбулентности.

Как и стандартная модель в физике частиц и стандартная космологическая модель, стандартная солнечная модель меняется со временем по мере необходимости обоснования новых теоретических или наблюдательных явлений.

Перенос энергии в Солнце

Солнце обладает ядром, в котором происходит лучистый перенос энергии, и конвективной внешней оболочкой. В ядре светимость, возникающая при протекании ядерных реакций, переносится во внешние слои в основном посредством излучения. Однако во внешних слоях градиент температуры настолько велик, что лучистый перенос не может переносить достаточное количество энергии. В результате перенос энергии осуществляется тепловой конвекцией, при которой более горячее вещество переносится к поверхности звезды. Поскольку на поверхности происходит охлаждение, то вещество погружается обратно вглубь конвективной зоны и снова разогревается на границе с областью лучистого переноса.

В солнечной модели, как описано в теории строения звёзд, рассматривается плотность ρ(r){\displaystyle \scriptstyle \rho (r)}, температура T(r), полное давление (вещества и излучения) P(r), светимость l(r) и темп создания энергии в расчёте на единицу массы ε(r) в сферической оболочке толщины dr на расстоянии r от центра звезды.

Лучистый перенос энергии описывается уравнением градиента температуры:

dTdr=−3κρl16πr2σT3,{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 16\pi r^{2}\sigma T^{3}},}

где κ являтся показателем непрозрачности вещества, σ — постоянная Стефана-Больцмана, постоянная Больцмана принята за единицу.

Конвекция описывается в терминах теории длины перемешивания^[5] с использованием соответствующего уравнения для градиента температуры при адиабатической конвекции:

dTdr=(1−1γ)TPdPdr,{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},}

где γ = c_p / c_v — показатель адиабаты. Для полностью ионизованного идеального газа показатель адиабаты γ = 5/3.

Вблизи нижней границы конвективной зоны Солнца конвекция является адиабатической, но вблизи поверхности это не так.

Моделирование конвекции вблизи поверхности

Более реалистичное описание верхней части конвективной зоны становится возможным в рамках подробного трёхмерного зависящего от времени гидродинамического моделирования с учётом лучистого переноса в атмосфере.^[6] Моделирование такого рода успешно воспроизводит наблюдаемую поверхностную структуру солнечной грануляции,^[7] а также детали на профилях линий в спектре излучения Солнца без использования параметрических моделей турбулентности.^[8] Моделирование описывает только малую долю солнечного радиуса и занимает слишком много вычислительного времени, поэтому его не включают в полное моделирование Солнца. Экстраполяция усреднённых результатов моделирования в адиабатической области конвективной зоны с помощью теории длины перемешивания показывает, что адиабата, полученная при моделировании, согласуется с глубиной конвективной зоны Солнца, определённой методами гелиосейсмологии.^[9] Обобщение теории длины перемешивания, включающее влияние турбулентного давления и кинетической энергии, основанное на результатах численного моделирования, также было разработано.^[10]

Уравнения состояния

Численное моделирование дифференциальных уравнений строения звёзд требует решения уравнений состояния для давления, непрозрачности и темпа энерговыделения, как описано в теории строения звёзд, связывающей эти величины с плотностью, температурой и химическим составом.

Гелиосейсмология

Гелиосейсмология изучает волновые колебания в Солнце. Изменения в распространении этих волн в Солнце выявляют внутреннюю структуру Солнца и позволяют астрофизикам разработать очень подробные профили для условий внутри Солнца. В частности, можно определить расположение конвективной зоны во внешних слоях Солнца, а сведения о ядре Солнца в совокупности с методами стандартной солнечной модели позволяют оценить возраст Солнца независимо от метода оценивания возраста по возрасту старейших метеоритов.^[11]

Формирование нейтрино

Водород превращается в гелий в ходе некоторых реакций в Солнце. Большинство нейтрино создаются при протон-протонных реакциях, в которых четыре протона переходят в два протона, два нейтрона, два позитрона и два электронных нейтрино. Нейтрино также создаются в рамках CNO-цикла, но этот процесс существенно менее эффективен в Солнце в отличие от других звёзд.

Большинство нейтрино создаются в Солнце в рамках первого шага протон-протонной цепочки, но их энергия настолько мала (<0.425 МэВ),^[12] что их сложно обнаружить. Редкая вариация протон-протонного цикла создаёт нейтрино при синтезе бора-8 при максимальной энергии приблизительно 15 МэВ, и эти нейтрино обнаружить проще всего. Очень редкое взаимодействие создаёт нейтрино высоких энергий. Максимальная энергия равна 18 МэВ.

Все описанные выше взаимодействия создают нейтрино с некоторым спектром энергий. Электронный захват ⁷Be создаёт нейтрино с энергией около 0,862 МэВ (~90%) или 0,384 МэВ (~10%).^[12]

Обнаружение нейтрино

Слабое взаимодействие нейтрино с другими частицами означает, что большинство нейтрино, создающихся в ядре Солнца, может пролететь Солнце, не испытывая поглощения. Следовательно, становится возможным наблюдение ядра Солнца непосредственно при наблюдении данных нейтрино.

История

Первым эксперимент по успешному обнаружению космических нейтрино — хлор-аргоновый эксперимент — был разработан Реймондом Дейвисом, в котором нейтрино обнаруживались при наблюдении перехода ядер атомов хлора в ядра радиоактивного аргона в большом объёме перхлорэтилена. Число зарегистрированных нейтрино не дало информации о том, откуда именно пришли данные нейтрино. В эксперименте была обнаружена только треть от предсказанного стандартной моделью количества нейтрино, данное расхождение теории и наблюдений получило название проблемы солнечных нейтрино.

Хотя в наши дни известно, что в ходе хлор-аргонного эксперимента действительно были обнаружены нейтрино, но во времена эксперимента некоторые физики сомневались в полученных результатах, поскольку не доверяли подобным радиохимическим методам. Более однозначное регистрирование солнечных нейтрино проводилось в рамках эксперимента Камиоканде-II, в котором регистрация происходила на водяном черенковском детекторе с низким порогом энергии для обнаружения нейтрино при нейтринно-электронном эластичном рассеянии. При взаимодействии в ходе эластичного рассеяния электроны, вылетающие из точки реакции, строго указывают направление движения нейтрино. Способность указывать назад на Солнце являлась первым являлась первым убедительным доказательством того, что Солнце вырабатывает энергию при ядерных реакциях в центре. Поскольку нейтрино, обнураженные в эксперименте Камиоканде-II, явно возникли в Солнце, то можно было снова сопоставить наблюдаемое количество нейтрино с теоретическим. Количество обнаруженных нейтрино оказалось вдвое меньшим, чем теоретическое.

[12] Водяные черенковские детекторы обнаруживают нейтрино только с энергиями выше 5 МэВ, а радиохимические эксперименты позволяли выявить нейтрино с менее высокими энергиями (0,8 МэВ для хлора, 0,2 МэВ для галлия), что стало причиной расхождения в соотношении доли выявленных нейтрино.

Протон-протонные цепочки

Все нейтрино из протон-протонных цепочек реакций были обнаружены, за исключением нейтрино высоких энергий. Были применены три вида методов. Методы радиохимии, использованные в экспериментах Homestake, Gallex, GNO и SAGE, позволили измерить поток нейтрино с энергией, выше минимальной. Детектор SNO использовал рассеяние на дейтерии, позволившее измерить энергию отдельных явлений и, следовательно, определять отдельные компоненты теоретического потока нейтрино. Камиоканде,Супер-Камиоканде, SNO, Borexino и KamLAND использовали упругое рассеяние на электронах, позволившее измерить энергию нейтрино. Нейтрино бора-8 зарегистрированы в экспериментах Камиоканде, Супер-Камиоканде, SNO, Borexino, KamLAND. Нейтрино бериллия-7 и протон-протонных цепочек были до настоящего времени обнаружены только Borexino.

Нейтрино с высокой энергией

Нейтрино с самыми высокими энергиями до сих пор не наблюдались вследствие малого потока по сравнению с потоком нейтрино бора-8, поэтому на их поток существуют лишь ограничения сверху. Пока ни один эксперимент не обладал необходимой чувствительностью для наблюдения предсказанного стандартной моделью потока нейтрино.

CNO-цикл

Нейтрино, возникшие в CNO-цикле, как предполагается, будут обладать наблюдаемыми проявлениями с энергиями ниже 1 МэВ. Они на данный момент не наблюдались вследствие наличия фонового шума. Сверхточные сцинцилляционные приёмники обладают возможностью измерить предсказанный моделью поток. Обнаружение нейтрино такого типа возможно в эксперименте Borexino; предполагается также, что такие нейтрино будут обнаружены в экспериментах SNO+, LENA и JUNO, которые будут использовать те же принципы, что и Borexino.

Будущие эксперименты

Хотя радиохимические эксперименты наблюдали нейтрино протон-протонных цепочек и Бериллия-7, всё же измерялись только интегральные потоки. Целью же экспериментов является обнаружение нейтрино бериллия-7 в эксперименте, в котором чувствительность приборов позволит определять отдельные нейтрино. В таком случае станет возможной проверка эффекта Михеева — Смирнова — Вольфенштейна. Поскольку некоторые экзотические модели также способны объяснить дефицит солнечных нейтрино, то непосредственное наблюдение эффекта Михеева — Смирнова — Вольфенштейна позволит окончательно разрешить проблему солнечных нейтрино.

Предположения о температуре в ядре

Поток нейтрино бора-8 очень чувствителен к температуре в ядре Солнца, ϕ(8B)∝T25{\displaystyle \phi (^{8}B)\propto T^{25}}.

[13] По этой причине точное измерение потока нейтрино бора-8 можно будет применить в стандартной солнечной модели для получения оценки температуры ядра Солнца. Такую оценку выполнили Фиорентини и Риччи после получения первых результатов SNO, величина температуры составила Tsun=15.7×106K±1%{\displaystyle T_{\text{sun}}=15.7\times 10^{6}\;{\text{K}}\;\pm 1\%} на основе потока нейтрино 5.2·10⁶/см²·s.^[14]

Уменьшение содержания лития на поверхности Солнца

Модель эволюции Солнца хорошо предсказывает химический состав поверхности Солнца за исключением содержания лития (Li). Поверхностное содержание лития на Солнце в 140 раз меньше, чем значение для протозвёзд (то есть первоначальное содержание лития на стадии рождения Солнца),^[15] хотя температура в основании конвективной зоны недостаточно горячая для сжигания и, следовательно, уменьшения содержания лития.^[16] Данное несоответствие называется проблемой содержания лития в Солнце. В звёздах типа Солнца одного возраста, массы и металличности содержание лития может варьироваться в широких пределах. Наблюдения несмещённых выборок звёзд данного типа как при наличии, так и при отсутствии планетных систем показало, что обладающие планетами звёзды обладают менее, чем 1%-м содержанием лития относительно первоначального, а в остальных звёздах у половины содержание лития в десятки раз больше. Предполагается, что наличие планет может увеличить величину смешивания и углубить конвективную зону до такой протяжённости, при которой литий может гореть. Возможным механизмом может являться влияние планет на изменение углового момента звезды, что изменяет параметры вращения звезды по сравнению с аналогичными звёздами без планет. В случае Солнца произошло замедление вращения.^[17] Для определения того, в каких случаях модель перестаёт быть корректной, требуются дополнительные исследования. Точность современных гелиосейсмологических исследований внутренней структуры Солнца показывает, что стандартная солнечная модель должна претерпеть некоторые изменения.

Примечания

↑ Guenther, D.B. (April 1989). «Age of the sun». Astrophysical Journal 339: 1156–1159. DOI:10.1086/167370. Bibcode: 1989ApJ…339.1156G.
↑ ¹ ² ³
↑ ¹ ² ³ Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics, Addison-Wesley (2007)
↑ Sackmann, I.-Juliana (November 1993). «Our Sun. III. Present and Future». Astrophysical Journal 418: 457–468. DOI:10.1086/173407. Bibcode: 1993ApJ…418..457S.
↑ Hansen, Carl J. Stellar Interiors / Carl J. Hansen, Kawaler, Trimble. — 2nd. — Springer, 2004. — ISBN 0-387-20089-4.
↑ Stein, R.F. (May 1998). «Simulations of Solar Granulation. I. General Properties». Astrophysical Journal 499 (2): 914–+. DOI:10.1086/305678. Bibcode: 1998ApJ…499..914S.
↑ Nordlund, A. (December 1997). «Stellar Convection; general properties» 225: 79–103. DOI:10.1007/978-94-011-5167-2_9. Bibcode: 1997ASSL..225…79N.
↑ Asplund, M. (July 2000). «Line formation in solar granulation. I. Fe line shapes, shifts and asymmetries». Astronomy and Astrophysics 359: 729–742. arXiv:astro-ph/0005320. Bibcode: 2000A&A…359..729A.
↑ Rosenthal, C.S. (November 1999). «Convective contributions to the frequencies of solar oscillations». Astronomy and Astrophysics 351: 689–700. arXiv:astro-ph/9803206. Bibcode: 1999A&A…351..689R.
↑ Li, L.H. (March 2002). «Inclusion of Turbulence in Solar Modeling». The Astrophysical Journal 567 (2): 1192–1201. arXiv:astro-ph/0109078. DOI:10.1086/338352. Bibcode: 2002ApJ…567.1192L.
↑ A. Bonanno (2002). «The age of the Sun and the relativistic corrections in the EOS». Astronomy and Astrophysics 390 (3). arXiv:astro-ph/0204331. DOI:10.1051/0004-6361:20020749. Bibcode: 2002A&A…390.1115B.
↑ ¹ ² ³ Bahcall, John Solar Neutrino Viewgraphs. Institute for Advanced Study School of Natural Science. Проверено 11 июля 2006.
↑ Bahcall, John (2002). «How many σ’s is the solar neutrino effect?». Physical Review C 65 (1). arXiv:hep-ph/0108147. DOI:10.1103/PhysRevC.65.015802. Bibcode: 2002PhRvC..65a5802B.
↑ Fiorentini, G. (2002). «What have we learnt about the Sun from the measurement of the 8B neutrino flux?». Physics Letters B 526 (3–4): 186–190. arXiv:astro-ph/0111334. DOI:10.1016/S0370-2693(02)01159-0. Bibcode: 2002PhLB..526..186F.
↑ Anders, E. (January 1989). «Abundances of the elements – Meteoritic and solar». Geochimica et Cosmochimica Acta 53 (1): 197–214. DOI:10.1016/0016-7037(89)90286-X. Bibcode: 1989GeCoA..53..197A.
↑ Maeder, A., Physics, Formation and Evolution of Rotating Stars. Astron. And Astrophys. Library, Springer Berlin Heidelberg, (2009).
↑ Israelian, G. (November 2009). «Enhanced lithium depletion in Sun-like stars with orbiting planets». Nature 462 (7270): 189–191. arXiv:0911.4198. DOI:10.1038/nature08483. PMID 19907489. Bibcode: 2009Natur.462..189I.

Ссылки

wikiredia.ru

Стандартная солнечная модель — Википедия

Калибровка солнечной модели

Видео по теме

Численное моделирование уравнений звёздной структуры

Эволюция Солнца

[3]

dLdr=4πr2ρ(ϵ−ϵν).{\displaystyle {\frac {dL}{dr}}=4\pi r^{2}\rho \left(\epsilon -\epsilon _{\nu }\right).}

Цели стандартной солнечной модели

Цели создания стандартной солнечной модели следующие:

предоставление оценки содержания гелия и величины масштаба перемешивания при согласовании параметров модели с оценками светимости и радиуса звезды в том же возрасте, что и Солнце.
предоставление способа оценки более сложных моделей с дополнительными эффектами, такими как вращение, магнитные поля и диффузия или уточнение явления конвекции, моделирование турбулентности.

Перенос энергии в Солнце

Лучистый перенос энергии описывается уравнением градиента температуры:

dTdr=−3κρl16πr2σT3,{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 16\pi r^{2}\sigma T^{3}},}

dTdr=(1−1γ)TPdPdr,{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},}

где γ = c_p / c_v — показатель адиабаты. Для полностью ионизованного идеального газа показатель адиабаты γ = 5/3.

Моделирование конвекции вблизи поверхности

Уравнения состояния

Гелиосейсмология

Формирование нейтрино

Обнаружение нейтрино

История

Решение проблемы солнечных нейтрино было экспериментально получено в обсерватории Садбери (SNO). Радиохимические эксперименты оказались чувствительными только к электронным нейтрино, и сигнал в водных черенковских экспериментах также в основном происходил при регистрации электронных нейтрино. Эксперимент в Садбери, напротив, был чувствителен ко всем трём видам нейтрино. При совместном измерении потока электронных нейтрино и полного потока нейтрино эксперимент показал, что понижение количества регистрируемых нейтрино происходило из-за эффекта Михеева — Смирнова — Вольфенштейна.^[12] Водяные черенковские детекторы обнаруживают нейтрино только с энергиями выше 5 МэВ, а радиохимические эксперименты позволяли выявить нейтрино с менее высокими энергиями (0,8 МэВ для хлора, 0,2 МэВ для галлия), что стало причиной расхождения в соотношении доли выявленных нейтрино.

Протон-протонные цепочки

Нейтрино с высокой энергией

CNO-цикл

Будущие эксперименты

Предположения о температуре в ядре

Поток нейтрино бора-8 очень чувствителен к температуре в ядре Солнца, ϕ(8B)∝T25{\displaystyle \phi (^{8}B)\propto T^{25}}.^[13] По этой причине точное измерение потока нейтрино бора-8 можно будет применить в стандартной солнечной модели для получения оценки температуры ядра Солнца. Такую оценку выполнили Фиорентини и Риччи после получения первых результатов SNO, величина температуры составила Tsun=15.7×106K±1%{\displaystyle T_{\text{sun}}=15.7\times 10^{6}\;{\text{K}}\;\pm 1\%} на основе потока нейтрино 5.2·10⁶/см²·s.^[14]

Уменьшение содержания лития на поверхности Солнца

Примечания

↑ Guenther, D.B. (April 1989). «Age of the sun». Astrophysical Journal 339: 1156–1159. DOI:10.1086/167370. Bibcode: 1989ApJ…339.1156G.
↑ ¹ ² ³
↑ ¹ ² ³ Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics, Addison-Wesley (2007)
↑ Sackmann, I.-Juliana (November 1993). «Our Sun. III. Present and Future». Astrophysical Journal 418: 457–468. DOI:10.1086/173407. Bibcode: 1993ApJ…418..457S.
↑ Hansen, Carl J. Stellar Interiors / Carl J. Hansen, Kawaler, Trimble. — 2nd. — Springer, 2004. — ISBN 0-387-20089-4.
↑ Stein, R.F. (May 1998). «Simulations of Solar Granulation. I. General Properties». Astrophysical Journal 499 (2): 914–+. DOI:10.1086/305678. Bibcode: 1998ApJ…499..914S.
↑ Nordlund, A. (December 1997). «Stellar Convection; general properties» 225: 79–103. DOI:10.1007/978-94-011-5167-2_9. Bibcode: 1997ASSL..225…79N.
↑ Asplund, M. (July 2000). «Line formation in solar granulation. I. Fe line shapes, shifts and asymmetries». Astronomy and Astrophysics 359: 729–742. arXiv:astro-ph/0005320. Bibcode: 2000A&A…359..729A.
↑ Rosenthal, C.S. (November 1999). «Convective contributions to the frequencies of solar oscillations». Astronomy and Astrophysics 351: 689–700. arXiv:astro-ph/9803206. Bibcode: 1999A&A…351..689R.
↑ Li, L.H. (March 2002). «Inclusion of Turbulence in Solar Modeling». The Astrophysical Journal 567 (2): 1192–1201. arXiv:astro-ph/0109078. DOI:10.1086/338352. Bibcode: 2002ApJ…567.1192L.
↑ A. Bonanno (2002). «The age of the Sun and the relativistic corrections in the EOS». Astronomy and Astrophysics 390 (3). arXiv:astro-ph/0204331. DOI:10.1051/0004-6361:20020749. Bibcode: 2002A&A…390.1115B.
↑ ¹ ² ³ Bahcall, John Solar Neutrino Viewgraphs. Institute for Advanced Study School of Natural Science. Проверено 11 июля 2006.
↑ Bahcall, John (2002). «How many σ’s is the solar neutrino effect?». Physical Review C 65 (1). arXiv:hep-ph/0108147. DOI:10.1103/PhysRevC.65.015802. Bibcode: 2002PhRvC..65a5802B.
↑ Fiorentini, G. (2002). «What have we learnt about the Sun from the measurement of the 8B neutrino flux?». Physics Letters B 526 (3–4): 186–190. arXiv:astro-ph/0111334. DOI:10.1016/S0370-2693(02)01159-0. Bibcode: 2002PhLB..526..186F.
↑ Anders, E. (January 1989). «Abundances of the elements – Meteoritic and solar». Geochimica et Cosmochimica Acta 53 (1): 197–214. DOI:10.1016/0016-7037(89)90286-X. Bibcode: 1989GeCoA..53..197A.
↑ Maeder, A., Physics, Formation and Evolution of Rotating Stars. Astron. And Astrophys. Library, Springer Berlin Heidelberg, (2009).
↑ Israelian, G. (November 2009). «Enhanced lithium depletion in Sun-like stars with orbiting planets». Nature 462 (7270): 189–191. arXiv:0911.4198. DOI:10.1038/nature08483. PMID 19907489. Bibcode: 2009Natur.462..189I.

Ссылки

wikipedia.green

Стандартная солнечная модель Википедия

Калибровка солнечной модели[ | ]

Численное моделирование уравнений звёздной структуры[

ru-wiki.ru

Интерактивная модель Солнца Helioviewer

А что мы знаем о Солнце с астрономической точки зрения? Большинство людей этот вопрос поставит в затруднительное положение. Ведь, скорее всего знания о нем будут отрывистые, не составляющие определенную систему. А слова «протуберанец», «солнечный ветер», «корона» вовсе могут вызвать недоумение.

Дать ответы на эти и многие другие вопросы призвана интерактивная модель Солнца. Это программа, работающая в сети Интернет и предоставляющая информацию о нашей звезде по данным космической программы Helioviewer.

Что мы знаем о нашей звезде

Мы живем на планете Земля, которая является составной частью Солнечной Системы – группы планет, вращающихся вокруг одного центра – Солнца. А что же нам известно о нем? В первую очередь, это самая близкая к нам звезда. Пусть она и не самая большая и не самая яркая на нашем небосводе по астрономическим меркам, но ее роль невозможно переоценить. Согревая своими лучами нашу Землю, однажды Солнце позволила появиться жизни на ней. Наверняка именно поэтому испокон веков все культуры мира почитают наше светило. Даже сегодня, в век технологического и научного прорыва, из миллионов видимых звезд только Солнце воспринимается больше, чем просто бездушный раскаленных газовый шар.

Интерактивная модель Солнца

Возможен выбор снимка за определенное число и дату. При выборе промежутка времени возможен просмотр видео.

Возможности приложения

Данная программа предоставляет пользователям как описательную, так и графическую информацию. Последняя представляет наибольший интерес, т.к. позволяет визуально познакомиться с Солнцем, основными его составляющими. В программе предусмотрено вращение звезды при помощи движения мыши. Также перемещением ползунка справа можно осуществить приближение и удаление изображения.

Помимо этого вы можете увидеть динамику солнечной активности. Пользователь может задать начальные и конечные параметры и просмотреть результат.

Приложение позволяет сформировать представление о нашем светиле и стать на шаг ближе к пониманию загадок космоса.

spacegid.com

Стандартная солнечная модель — Википедия Переиздание // WIKI 2

Калибровка солнечной модели

[2] Для создания более точной модели требуется лучше знать параметры диффузии.

Численное моделирование уравнений звёздной структуры

Эволюция Солнца

dLdr=4πr2ρ(ϵ−ϵν).{\displaystyle {\frac {dL}{dr}}=4\pi r^{2}\rho \left(\epsilon -\epsilon _{\nu }\right).}

Цели стандартной солнечной модели

Цели создания стандартной солнечной модели следующие:

предоставление оценки содержания гелия и величины масштаба перемешивания при согласовании параметров модели с оценками светимости и радиуса звезды в том же возрасте, что и Солнце.
предоставление способа оценки более сложных моделей с дополнительными эффектами, такими как вращение, магнитные поля и диффузия или уточнение явления конвекции, моделирование турбулентности.

Перенос энергии в Солнце

Лучистый перенос энергии описывается уравнением градиента температуры:

dTdr=−3κρl16πr2σT3,{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 16\pi r^{2}\sigma T^{3}},}

dTdr=(1−1γ)TPdPdr,{\displaystyle {{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},}

где γ = c_p / c_v — показатель адиабаты. Для полностью ионизованного идеального газа показатель адиабаты γ = 5/3.

Моделирование конвекции вблизи поверхности

Уравнения состояния

Гелиосейсмология

Формирование нейтрино

Обнаружение нейтрино

История

Протон-протонные цепочки

Нейтрино с высокой энергией

CNO-цикл

Будущие эксперименты

Предположения о температуре в ядре

Уменьшение содержания лития на поверхности Солнца

Примечания

↑ Guenther, D.B. (April 1989). «Age of the sun». Astrophysical Journal 339: 1156–1159. DOI:10.1086/167370. Bibcode: 1989ApJ…339.1156G.
↑ ¹ ² ³
↑ ¹ ² ³ Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics, Addison-Wesley (2007)
↑ Sackmann, I.-Juliana (November 1993). «Our Sun. III. Present and Future». Astrophysical Journal 418: 457–468. DOI:10.1086/173407. Bibcode: 1993ApJ…418..457S.
↑ Hansen, Carl J. Stellar Interiors / Carl J. Hansen, Kawaler, Trimble. — 2nd. — Springer, 2004. — ISBN 0-387-20089-4.
↑ Stein, R.F. (May 1998). «Simulations of Solar Granulation. I. General Properties». Astrophysical Journal 499 (2): 914–+. DOI:10.1086/305678. Bibcode: 1998ApJ…499..914S.
↑ Nordlund, A. (December 1997). «Stellar Convection; general properties» 225: 79–103. DOI:10.1007/978-94-011-5167-2_9. Bibcode: 1997ASSL..225…79N.
↑ Asplund, M. (July 2000). «Line formation in solar granulation. I. Fe line shapes, shifts and asymmetries». Astronomy and Astrophysics 359: 729–742. arXiv:astro-ph/0005320. Bibcode: 2000A&A…359..729A.
↑ Rosenthal, C.S. (November 1999). «Convective contributions to the frequencies of solar oscillations». Astronomy and Astrophysics 351: 689–700. arXiv:astro-ph/9803206. Bibcode: 1999A&A…351..689R.
↑ Li, L.H. (March 2002). «Inclusion of Turbulence in Solar Modeling». The Astrophysical Journal 567 (2): 1192–1201. arXiv:astro-ph/0109078. DOI:10.1086/338352. Bibcode: 2002ApJ…567.1192L.
↑ A. Bonanno (2002). «The age of the Sun and the relativistic corrections in the EOS». Astronomy and Astrophysics 390 (3). arXiv:astro-ph/0204331. DOI:10.1051/0004-6361:20020749. Bibcode: 2002A&A…390.1115B.
↑ ¹ ² ³ Bahcall, John Solar Neutrino Viewgraphs. Institute for Advanced Study School of Natural Science. Проверено 11 июля 2006.
↑ Bahcall, John (2002). «How many σ’s is the solar neutrino effect?». Physical Review C 65 (1). arXiv:hep-ph/0108147. DOI:10.1103/PhysRevC.65.015802. Bibcode: 2002PhRvC..65a5802B.
↑ Fiorentini, G. (2002). «What have we learnt about the Sun from the measurement of the 8B neutrino flux?». Physics Letters B 526 (3–4): 186–190. arXiv:astro-ph/0111334. DOI:10.1016/S0370-2693(02)01159-0. Bibcode: 2002PhLB..526..186F.
↑ Anders, E. (January 1989). «Abundances of the elements – Meteoritic and solar». Geochimica et Cosmochimica Acta 53 (1): 197–214. DOI:10.1016/0016-7037(89)90286-X. Bibcode: 1989GeCoA..53..197A.
↑ Maeder, A., Physics, Formation and Evolution of Rotating Stars. Astron. And Astrophys. Library, Springer Berlin Heidelberg, (2009).
↑ Israelian, G. (November 2009). «Enhanced lithium depletion in Sun-like stars with orbiting planets». Nature 462 (7270): 189–191. arXiv:0911.4198. DOI:10.1038/nature08483. PMID 19907489. Bibcode: 2009Natur.462..189I.

Ссылки

Эта страница в последний раз была отредактирована 15 июля 2018 в 12:26.

wiki2.org

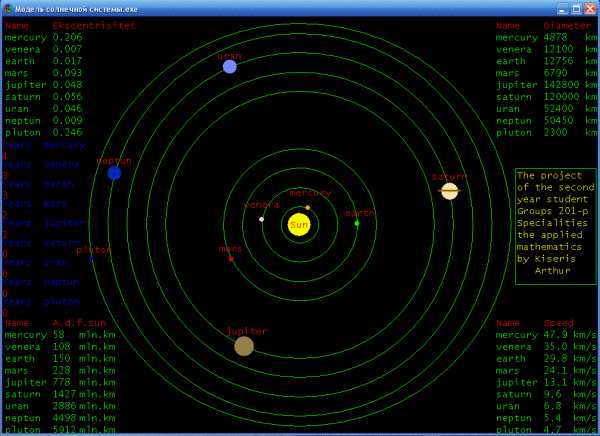Модель Солнечной системы | Основы программирования

Задача: отобразить солнечную систему;
Использованный API: GTK/GDK;
Среда разработки: Visual Studio 2008;

В этой картинке 9 анимированых объектов, 10 статический и 5 статических полей с информацией:
1. Планеты
2. Солнце
3. Орбиты планет
4. Поля с информацией о планетах

Изменение координат планет происходит при помощи функций sin и cos, делая круговые движения. Координаты планет системы вычисляются по формулам:

x[i]=a[i]*cos(t[i])+WIDTH/2;
y[i]=b[i]*sin(t[i])+HEIGHT/2;

где i — номер планеты по создаваемой базе данных
t — параметр, касательно которого изменяются координаты
WIDTH, HEIGHT — стандартные, минимальные размеры экрана
a,b — значение малой и большой полуосей.

Очевидно что орбиты планет имеют эллиптическую форму, которая зависит от эксцентриситета орбит. Но при попытки использовать масштабирование для создания модели, я столкнулся с невозможностью использования такого метода т.к. размеры некоторых планет во много раз превосходят другие. Поэтому пришлось использовать схематическую модель, базирующаяся на реальных характеристиках планет и их орбит. Скорость движения планет вычисляется относительно их реальных скоростей, уменьшив их в 1000 раз.

//Необходимые строки для подключения gtk в VS
#pragma comment(lib,"gthread-2.0.lib")
#pragma comment(lib,"gtk-win32-2.0.lib")
#pragma comment(lib,"glib-2.0.lib")
#pragma comment(lib,"gobject-2.0.lib")
#pragma comment(lib,"gdk-win32-2.0.lib")
#pragma comment(lib,"gdk_pixbuf-2.0.lib")
#pragma comment(lib,"pango-1.0.lib")
#pragma comment(lib,"pangowin32-1.0.lib")
#pragma comment(lib,"intl.lib")
 
#include <gtk/gtk.h>
#include <math.h>//для вычисления синусов и косинусов
#include <stdlib.h>
//Размеры окна
#define WIDTH 1000
#define HEIGHT 700
#define M_PI 3.14
#define OTSTUP 10
#define lim_planet 9
#define lim_name 15
#define interval 25//Интервал вызова ф-ии рисования солнечной системы
#define speed_change_t 0.001 //На сколько изменяется параметр t
 
char name[lim_planet][lim_name],change_num[50],type_name[lim_planet][2*lim_name],ch_num[lim_planet];
float e[lim_planet],r_e[lim_planet],t[9],k,v[lim_planet],r_v[lim_planet];
int d[lim_planet],r_d[lim_planet],a[lim_planet],r_a[lim_planet],b[lim_planet],x[lim_planet],y[lim_planet],i,me=77777,xs=5,ys=20;
int timer[lim_planet],xt[lim_planet],yt[lim_planet],num_change_t[lim_planet];
 
FILE *info=fopen("other_information.txt","rt");//файл с используемыми характеристиками планет
FILE *r_info=fopen("information.txt","rt");//файл с реальными характеристиками планет
 
GdkColor fclrs,bclr,clr;
GdkGC *gc;
 
gboolean destroy(GtkWidget *widget);
gint delete_event(GtkWidget *widget);
 
gboolean information(GtkWidget *widget);//ф-ия создавания полей с информацией о планетах
gboolean run_planet(GtkWidget *widget);//ф-ия рисования слнечной системы
 
 
 
 
int main(int arge, char **argv)
{
	xt[0]=0;yt[0]=240;
	for(i=1;i<lim_planet;i++) {yt[i]=yt[i-1]+33;xt[i]=0;}
	//Создание базы с информацией
	for(i=0;i<5;i++)
	{fscanf(r_info,"%s",type_name[i]);}
	for(i=0;i<lim_planet;i++)
	{
		fscanf(r_info,"%f",&r_e[i]);
		fscanf(r_info,"%d",&r_a[i]);
		fscanf(r_info,"%d",&r_d[i]);
		fscanf(r_info,"%f",&r_v[i]);
	}fclose(r_info);
	for(i=0;i<lim_planet;i++)
	{
		fscanf(info,"%s",name[i]);
		fscanf(info,"%f",&e[i]);
		fscanf(info,"%d",&a[i]);
		fscanf(info,"%d",&d[i]);
		fscanf(info,"%f",&v[i]);
 
	}fclose(info);
 
	//Увеличение эксцентриситета планет для зрелещности изображения
	for(i=0;i<lim_planet;i++) e[i]*=1.2;
 
	//Вычисление максимального значения оси относительно экрана
	b[8]=HEIGHT/2-OTSTUP;
 
	//k=b(плутона максимальное компьютерное)/b(плутона реальное)
	k=b[8]/(a[8]*sqrt(1-(e[8]*e[8])));
 
	//Уменьшение значений полуосей и диаметров планет согласно экрана и масштабирования
	for(i=0;i<lim_planet;i++) 
	{	
		a[i]*=k;
		b[i]=a[i]*sqrt(1-e[i]*e[i]);
		d[i]/=200;
	}
 
 
 
	gtk_init(&arge,&argv);
	GtkWidget *window = gtk_window_new(GTK_WINDOW_TOPLEVEL);
	gtk_widget_set_size_request(window,WIDTH,HEIGHT);
	g_signal_connect(G_OBJECT(window),"destroy",G_CALLBACK(destroy),NULL);
	g_signal_connect(G_OBJECT(window),"delete_event",G_CALLBACK(delete_event),NULL);
	gdk_color_parse("black",&clr);
	gtk_widget_modify_bg(window,GTK_STATE_NORMAL,&clr);
	g_signal_connect(G_OBJECT(window),"expose_event",G_CALLBACK(run_planet),NULL);
 
	g_timeout_add(interval,(GSourceFunc)run_planet,(gpointer)window);
	g_timeout_add(interval,(GSourceFunc)information,(gpointer)window);
 
	gtk_widget_show_all(window);
	gtk_main();
 
	return 0;
}
 
gboolean destroy(GtkWidget *widget)
{
	return FALSE;
}
 
gint delete_event(GtkWidget *widget)
{
	gtk_main_quit();
	return 1;
}
 
 
gboolean information(GtkWidget *widget)
{
	gc = widget->style->fg_gc[GTK_WIDGET_STATE(widget)];
	GdkFont *font=gdk_fontset_load("Lucida Console");
 
	for(i=0;i<lim_planet;i++)
	{
		gdk_gc_set_rgb_fg_color(gc,&clr);
		sprintf(ch_num,"%d",timer[i]);
		gdk_draw_string(widget->window,font,gc,xt[i],yt[i],ch_num);
		//проверка на изменение времени на планете, если число изменений(вычесленных в ручную) совпадает с данным числом, то год прошёл 
		switch(i)
		{
		case 0:
			{
				if(num_change_t[0]==131) 
				{
					num_change_t[0]=0; 
					timer[0]++;
				}break;
			}
		case 1:
			{
				if(num_change_t[1]==179) 
				{
					num_change_t[1]=0; 
					timer[1]++;
				}break;
			}
		case 2:
			{
				if(num_change_t[2]==210) 
				{
					num_change_t[2]=0; 
					timer[2]++;
				}break;
			}
		case 3:
			{
				if(num_change_t[3]==261) 
				{
					num_change_t[3]=0; 
					timer[3]++;
				}break;
			}
		case 4:
			{
				if(num_change_t[4]==479) 
				{
					num_change_t[4]=0; 
					timer[4]++;
				}break;
			}
		case 5:
			{
				if(num_change_t[5]==654) 
				{
					num_change_t[5]=0; 
					timer[5]++;
				}break;
			}
		case 6:
			{
				if(num_change_t[6]==924) 
				{
					num_change_t[6]=0; 
					timer[6]++;
				}break;
			}
		case 7:
			{
				if(num_change_t[7]==1162) 
				{
					num_change_t[7]=0; 
					timer[7]++;
				}break;
			}
		case 8:
			{
				if(num_change_t[8]==1281) 
				{
					num_change_t[8]=0; 
					timer[8]++;
				}break;
			}
		}
		//Создание поля с годами на планетах
		fclrs.pixel = 0;
		fclrs.red = 0;
		fclrs.green = 0;
		fclrs.blue = 0xFFFF;
		gdk_gc_set_rgb_fg_color(gc,&fclrs);
		gdk_draw_string(widget->window,font,gc,xt[i],yt[i]-20,"Years ");
		gdk_draw_string(widget->window,font,gc,xt[i]+70,yt[i]-20,name[i]);
		sprintf(ch_num,"%d",timer[i]);
		fclrs.pixel = 0;
		fclrs.red = 0xFFFF;
		fclrs.green = 0;
		fclrs.blue = 0;
		gdk_gc_set_rgb_fg_color(gc,&fclrs);
		gdk_draw_string(widget->window,font,gc,xt[i],yt[i],ch_num);
	}
	//создание лэйбочки с информацией о хозяине проекта
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_line(widget->window,gc,862,255,997,255);
	gdk_draw_line(widget->window,gc,862,450,997,450);
	gdk_draw_line(widget->window,gc,862,255,862,450);
	gdk_draw_line(widget->window,gc,997,255,997,450);
	fclrs.pixel = 0;fclrs.red = 0xFA00;fclrs.green = 0xFD00;fclrs.blue = 0;gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_string(widget->window,font,gc,865,272,"The project");
	gdk_draw_string(widget->window,font,gc,865,292,"of the second");
	gdk_draw_string(widget->window,font,gc,865,312,"year student");
	gdk_draw_string(widget->window,font,gc,865,332,"Groups 201-p");
	gdk_draw_string(widget->window,font,gc,865,352,"Specialities");
	gdk_draw_string(widget->window,font,gc,865,372,"the applied");
	gdk_draw_string(widget->window,font,gc,865,392,"mathematics");
	gdk_draw_string(widget->window,font,gc,865,412,"by Kiseris");
	gdk_draw_string(widget->window,font,gc,865,432,"   Arthur");
//Вывод первого поля, к-ое содержит информацию о эксцентриситете планет
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	xs=5;ys=20;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[0]);
	xs+=80;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[1]);
	xs=5;ys+=20;
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0x00FF;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	for(i=0,xs=5;i<9;i++,xs=5)
	{
		gdk_draw_string(widget->window,font,gc,xs,ys,name[i]);
		xs+=80;
		sprintf(change_num, "%3.3f",r_e[i]);
		gdk_draw_string(widget->window,font,gc,xs,ys,change_num);
		ys+=20;
	}
//Вывод второго поля, к-ое содержит информацию о среднем расстоянии планет от солнца
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	xs=5;ys=520;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[0]);
	xs+=80;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[2]);
	xs=5;ys+=20;
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0x00FF;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	for(i=0,xs=5;i<9;i++,xs=5)
	{
		gdk_draw_string(widget->window,font,gc,xs,ys,name[i]);
		xs+=80;
		sprintf(change_num, "%d",r_a[i]);
		gdk_draw_string(widget->window,font,gc,xs,ys,change_num);
		gdk_draw_string(widget->window,font,gc,xs+45,ys,"mln.km");
		ys+=20;
	}
//Вывод третего поля, к-ое содержит информацию о диаметре планет
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	xs=830;ys=20;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[0]);
	xs+=80;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[3]);
	xs=830;ys+=20;
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0x00FF;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	for(i=0,xs=830;i<9;i++,xs=830)
	{
		gdk_draw_string(widget->window,font,gc,xs,ys,name[i]);
		xs+=80;
		sprintf(change_num, "%d",r_d[i]);
		gdk_draw_string(widget->window,font,gc,xs,ys,change_num);
		gdk_draw_string(widget->window,font,gc,xs+40,ys,"   km");
		ys+=20;
	}
//Вывод четвёртого поля, к-ое содержит информацию о диаметре планет
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	xs=830;ys=520;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[0]);
	xs+=80;
	gdk_draw_string(widget->window,font,gc,xs,ys,type_name[4]);
	xs=830;ys+=20;
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0x00FF;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	for(i=0,xs=830;i<9;i++,xs=830)
	{
		gdk_draw_string(widget->window,font,gc,xs,ys,name[i]);
		xs+=80;
		sprintf(change_num, "%3.1f",r_v[i]);
		gdk_draw_string(widget->window,font,gc,xs,ys,change_num);
		gdk_draw_string(widget->window,font,gc,xs+40,ys," km/s");
		ys+=20;
	}
 
	return TRUE;
}
 
gboolean run_planet(GtkWidget *widget)
{
	gc = widget->style->fg_gc[GTK_WIDGET_STATE(widget)];
	GdkFont *font=gdk_fontset_load("Lucida Console");
 
//Стерание предыдущих планет и названия используя цвет фона(чёрный)
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
 
	gdk_draw_arc(widget->window,gc,TRUE,x[8]-d[8],y[8]-d[8],2*d[8],2*d[8],0,360*64);
	gdk_draw_string(widget->window,font,gc,x[8]-25,y[8]-10,name[8]);
	gdk_draw_arc(widget->window,gc,TRUE,x[7]-(d[7]/2),y[7]-(d[7]/2),d[7],d[7],0,360*64);	
	gdk_draw_string(widget->window,font,gc,x[7]-30,y[7]-16,name[7]);
	gdk_draw_arc(widget->window,gc,TRUE,x[6]-(d[6]/2),y[6]-(d[6]/2),d[6],d[6],0,360*64);	
	gdk_draw_string(widget->window,font,gc,x[6]-20,y[6]-13,name[6]);
	gdk_draw_arc(widget->window,gc,TRUE,x[5]-(d[5]/2),y[5]-(d[5]/2),d[5],d[5],0,360*64);
	gdk_draw_rectangle(widget->window,gc,TRUE,x[5]-(d[5]/2)-5,y[5]-3,d[5]+8,3);
	gdk_draw_string(widget->window,font,gc,x[5]-30,y[5]-20,name[5]);
	gdk_draw_arc(widget->window,gc,TRUE,x[4]-(d[4]/2),y[4]-(d[4]/2),d[4],d[4],0,360*64);	
	gdk_draw_string(widget->window,font,gc,x[4]-30,y[4]-20,name[4]);
	gdk_draw_arc(widget->window,gc,TRUE,x[3]-(d[3]/2),y[3]-(d[3]/2),d[3],d[3],0,360*64);
	gdk_draw_string(widget->window,font,gc,x[3]-20,y[3]-13,name[3]);
	gdk_draw_arc(widget->window,gc,TRUE,x[2]-(d[2]/2),y[2]-(d[2]/2),d[2],d[2],0,360*64);	
	gdk_draw_string(widget->window,font,gc,x[2]-20,y[2]-13,name[2]);
	gdk_draw_arc(widget->window,gc,TRUE,x[1]-(d[1]/2),y[1]-(d[1]/2),d[1],d[1],0,360*64);	
	gdk_draw_string(widget->window,font,gc,x[1]-30,y[1]-20,name[1]);
	gdk_draw_arc(widget->window,gc,TRUE,x[0]-(d[0]/2),y[0]-(d[0]/2),d[0],d[0],0,360*64);	
	gdk_draw_string(widget->window,font,gc,x[0]-30,y[0]-20,name[0]);
 
//Изменение координат 
	for(i=0;i<9;i++)
	{
		x[i]=a[i]*cos(t[i])+WIDTH/2;
		y[i]=b[i]*sin(t[i])+HEIGHT/2;
	}
 
//Отображение граней для осей СС
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0x00FF;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
 
	for(i=0;i<9;i++)
	{
		gdk_draw_arc(widget->window,gc,FALSE,WIDTH/2-a[i],HEIGHT/2-b[i],2*a[i],2*b[i],0,360*64);
	}
 
//Рисование новых рисунков с новыми координатами 
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0;
	fclrs.blue = 0xFFFF;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[8]-(d[8]/2),y[8]-(d[8]/2),d[8],d[8],0,360*64);
 
	fclrs.pixel = 0;
	fclrs.red = 0x0B00;
	fclrs.green = 0x2700;
	fclrs.blue = 0xB500;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[7]-(d[7]/2),y[7]-(d[7]/2),d[7],d[7],0,360*64);
 
	fclrs.pixel = 0;
	fclrs.red = 0x7900;
	fclrs.green = 0x8C00;
	fclrs.blue = 0xFF00;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[6]-(d[6]/2),y[6]-(d[6]/2),d[6],d[6],0,360*64);
 
	fclrs.pixel = 0;
	fclrs.red = 0xFC00;
	fclrs.green = 0xE400;
	fclrs.blue = 0xAC00;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[5]-(d[5]/2),y[5]-(d[5]/2),d[5],d[5],0,360*64);
	fclrs.pixel = 0;
	fclrs.red = 0x8F00;
	fclrs.green = 0x6500;
	fclrs.blue = 0x0200;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_rectangle(widget->window,gc,TRUE,x[5]-(d[5]/2)-5,y[5]-3,d[5]+8,3);
 
	fclrs.pixel = 0;
	fclrs.red = 0x9700;
	fclrs.green = 0x8000;
	fclrs.blue = 0x4900;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[4]-(d[4]/2),y[4]-(d[4]/2),d[4],d[4],0,360*64);
 
 
	fclrs.pixel = 0;
	fclrs.red = 0xDDDD;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[3]-(d[3]/2),y[3]-(d[3]/2),d[3],d[3],0,360*64);
 
	fclrs.pixel = 0;
	fclrs.red = 0;
	fclrs.green = 0xFFFF;
	fclrs.blue = 0x00DD;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[2]-(d[2]/2),y[2]-(d[2]/2),d[2],d[2],0,360*64);
 
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0xCCCC;
	fclrs.blue = 0xCCCC;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[1]-(d[1]/2),y[1]-(d[1]/2),d[1],d[1],0,360*64);
 
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0xA5AA;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,x[0]-(d[0]/2),y[0]-(d[0]/2),d[0],d[0],0,360*64);
 
//Рисование солнца
	fclrs.pixel = 0;
	fclrs.red = 0xFA00;
	fclrs.green = 0xFD00;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
	gdk_draw_arc(widget->window,gc,TRUE,e[8]*a[8]+a[8]+20,HEIGHT/2-20,40,40,0,360*64);
 
//Создания надписей
	fclrs.pixel = 0;
	fclrs.red = 0xFFFF;
	fclrs.green = 0;
	fclrs.blue = 0;
	gdk_gc_set_rgb_fg_color(gc,&fclrs);
 
	gdk_draw_string(widget->window,font,gc,x[8]-25,y[8]-10,name[8]);
	gdk_draw_string(widget->window,font,gc,x[7]-30,y[7]-16,name[7]);
	gdk_draw_string(widget->window,font,gc,x[6]-20,y[6]-13,name[6]);
	gdk_draw_string(widget->window,font,gc,x[5]-30,y[5]-20,name[5]);	
	gdk_draw_string(widget->window,font,gc,x[4]-30,y[4]-20,name[4]);
	gdk_draw_string(widget->window,font,gc,x[3]-20,y[3]-13,name[3]);
	gdk_draw_string(widget->window,font,gc,x[2]-20,y[2]-13,name[2]);
	gdk_draw_string(widget->window,font,gc,x[1]-30,y[1]-20,name[1]);
	gdk_draw_string(widget->window,font,gc,x[0]-30,y[0]-20,name[0]);
//Создания надписи	солнца	
	gdk_draw_string(widget->window,font,gc,e[8]*a[8]+a[8]+25,HEIGHT/2+5,"Sun");
	//увеличить счётчик изменений параметра у каждой планеты
	for(i=0;i<9;i++)
	{
		num_change_t[i]++;
	}
	//увеличение параметра согласно произведения реальной скорости планеты на опр. коофициент 
	for(i=0;i<9;i++)
	{
		t[i]+=speed_change_t*v[i];
	}
 
	return TRUE;
}

Ключевые слова:

Солнечная система

Вложение	Размер
солнечной системы.rar	1.26 Мб

www.opita.net

2.3. Модель солнца.

2.3. Модель солнца.

Очень интересно наблюдать за солнцем при помощи телескопа. Можно рассмотреть потемнение края солнечного диска, солнечные пятна, факельные поля и даже грануляцию.

Солнечные пятна это выбросы кусков магмы на некоторую высоту солнечной поверхности. Солнечные пятна появляются на поверхности Солнца неравномерно по времени и с разной интенсивностью (масса, скорость выделения). Поэтому пока нельзя точно определить период вращения звезды вокруг своей оси. Звезда по имени Солнце окутано, горячим и горящим газом, внешние слои которого на высоте солнечных пятен вращаются вокруг Солнца быстрее, чем сами пятна. Солнечные пятна совершают полный оборот вокруг Солнца за 27,5 дней (среднее значение). Точнее на экваторе за 25 дней, а удаляясь от экватора скорость солнечных пятен уменьшается и у полюсов равна примерно от 31 дней до 36 дней. Поэтому ученые решили, что Солнце вращается, каждые 25 дней на экваторе и медленнее вращается в более высоких широтах, до 35 дней в полюсах.

Чтобы рассмотреть наиболее характерные детали поверхности Солнца иногда советуют спроектировать изображение Солнца на экран в хорошо затемненной комнате и тогда можно рассмотреть Солнечное затмение, структуру пятен и факельные поля. Для этого изготавливается камера из черной бумаги, в которую помещается окулярная часть вместе с экраном, но рассматривать изображение можно только одному человеку.

Я предлагаю модель для демонстрации солнечных пятен из пенопласта. Она представляет собой укрепленную на демонстрационном экране полую сферу, внутри которой расположен источник света. Пористая структура модели обеспечивает зернистое строение поверхности, очень сходное с грануляцией.

Технология изготовления модели очень проста. На куске пенопласта толщиной 8-10 см проводится окружность радиусом 4-5 см. Острым ножом, заготовке придается форма полусферы. Окончательная отделка сводится к зачистке поверхности мелкозернистой шкуркой. В полусфере, со стороны её основания, аккуратно вырезается небольшая полость для источника света. Полость также имеет форму полусферы. Полусфера укрепляется на фанерном экране размером 50-50 см шурупами. В центре экрана высверливается отверстие, в которое вставляется электрический патрон. Для освещения полусферы используется автомобильная электролампа на 6-12В. Экран закрашивается краской или заклеивается бумагой темно-синего цвета.

В полусфере, с внешней стороны, остро заточенным концом тонкостенной металлической трубочки диаметром до 1 см вырезаем два отверстия одинаковой глубины (1,5-2 см) так, чтобы одно отверстие находилось в центре полусферы, а другое – вблизи её края. Стенки отверстий экранируются от внутреннего рассеянного света бумажными трубочками, вставленными в эти отверстия.

C олнечное пятно изображается не на полусфере, а на специальной пробке. Для которой в полусфере делается отверстие диаметром 5-6 мм и глубиной 10 мм. Пробка изготавливается из куска пенопласта, с которого предварительно срезается гладкий блестящий слой толщиной не более 1,5 мм. Высота пробки 10 мм. До полвины высота пробки имеет форму цилиндра, диаметр которого равен диаметру отверстия в полусфере. Другая половина делается конической, расширяющейся к срезу. Обжав коническую часть, пробку запрессовывают в отверстие. Затем, аккуратно подрезая пробку, острым ножом формуют в ней неглубокую воронку, на стенах которой тупым концом ножа делают прожилки, что обеспечивает более полное сходство с полутенью. Центральная часть пробки (тень пятна) закрашивается черной акварельной краской. Можно нанести на поверхность полусферы несколько пор. Лучше изобразить на полусфере два пятна – одно в центральной его части, другое – ближе к краю.

Для изображения на поверхности полусферы факелов ближе к её краям, там, где имеется потемнение, ножом срезаются несколько небольших площадок неправильной формы. Эти площадки будут светиться ярче, чем сама полусфера, создавая полную иллюзию факелов. Как показывать модель и демонстрировать на ней различные физические явления происходящие на Солнце я расскажу в практической части работы.

Фотографии модели солнца

<= Назад —— На главную —— Вперёд=>

sunny-light-star.narod.ru

Стандартная солнечная модель Википедия

Калибровка солнечной модели

Численное моделирование уравнений звёздной структуры

Эволюция Солнца

Цели стандартной солнечной модели

Перенос энергии в Солнце

Моделирование конвекции вблизи поверхности

Уравнения состояния

Гелиосейсмология

Формирование нейтрино

Обнаружение нейтрино

История

Протон-протонные цепочки

Нейтрино с высокой энергией

CNO-цикл

Будущие эксперименты

Предположения о температуре в ядре

Уменьшение содержания лития на поверхности Солнца

Примечания

Ссылки

Стандартная солнечная модель — Википедия

Калибровка солнечной модели

Видео по теме

Численное моделирование уравнений звёздной структуры

Эволюция Солнца

Цели стандартной солнечной модели

Перенос энергии в Солнце

Моделирование конвекции вблизи поверхности

Уравнения состояния

Гелиосейсмология

Формирование нейтрино

Обнаружение нейтрино

История

Протон-протонные цепочки

Нейтрино с высокой энергией

CNO-цикл

Будущие эксперименты

Предположения о температуре в ядре

Уменьшение содержания лития на поверхности Солнца

Примечания

Ссылки

Стандартная солнечная модель Википедия

Калибровка солнечной модели[ | ]

Численное моделирование уравнений звёздной структуры[

Интерактивная модель Солнца Helioviewer

Что мы знаем о нашей звезде

Интерактивная модель Солнца

Возможности приложения

Стандартная солнечная модель — Википедия Переиздание // WIKI 2

Калибровка солнечной модели

Численное моделирование уравнений звёздной структуры

Эволюция Солнца

Цели стандартной солнечной модели

Перенос энергии в Солнце

Моделирование конвекции вблизи поверхности

Уравнения состояния

Гелиосейсмология

Формирование нейтрино

Обнаружение нейтрино

История

Протон-протонные цепочки

Нейтрино с высокой энергией

CNO-цикл

Будущие эксперименты

Предположения о температуре в ядре

Уменьшение содержания лития на поверхности Солнца

Примечания

Ссылки

Модель Солнечной системы | Основы программирования

2.3. Модель солнца.

Добавить комментарий Отменить ответ